|
مسائل بهینهسازی توپولوژی 1-5- مقدمه |
|
ﺗﻼش ﺟﻬﺖ ﻳﺎﻓﺘﻦ ﻃﺮﺣﻲ ﻛﻪ داراي مناسبترین ویژگی باشد، سالهای ﻣﺘﻤﺎدي ذﻫﻦ ﻣﺤﻘﻘﻴﻦ را ﺑﻪ ﺧﻮد ﻣﺸﻐﻮل ﻛﺮده اﺳﺖ. بهینهسازی ﺗﻮﭘﻮﻟﻮژﻳﻜﻲ را میتوان بهعنوان روﺷﻲ ﺟﻬﺖ ﺗﻮزﻳﻊ ﺑﻬﻴﻨﻪ ﺟﺮم در ﻓﻀﺎي ﻃﺮاﺣﻲ ﺗﻌﺮﻳﻒ ﻛﺮد ﻛﻪ درنهایت ﺿﻤﻦ در ﻧﻈﺮ ﮔﺮﻓﺘن ﻗﻴﻮد ﺣﺎﻛﻢ ﺑﺮ ﻣﺴﺌﻠﻪ به ﺳﺎﺧﺘﺎر ﻣﻨﺎﺳﺐ دﺳﺖ مییابد. بهینهسازی ﺗﻮﭘﻮﻟﻮژﻳﻜﻲ ﺑﺎ ﻣﻄﺎﻟﻌﺎت ﻣﺎﻳﻜل ﺑﺮ روي اﻧﻮاع ﺧﺮﭘﺎﻫﺎ آﻏﺎز شد و در سالهای ﺑﻌﺪ ﺑﺎ اراﺋﻪ روشهای ﺑﺮ ﭘﺎﻳﻪ رﻳﺎﺿﻴﺎت، این ﻧﻮع بهینهسازی ﺑﻪ ﺷﻜﻞ گسترده¬تری مورداستفاده ﻗﺮار ﮔﺮﻓﺖ. هرچند ﻛﻪ اﻳﻦ روشها ﺑﺮاي ﻣﺴﺎﺋﻞ ﺑﺰرگ ﺑﺎ اﺑﻌﺎد واﻗﻌﻲ ﭼﻨﺪان ﻛﺎرآﻣﺪ ﻧﺒﻮدند، اﻣﺎ در ﻣﻘﺎﺑﻞ ﺳﺎﻳﺮ روش¬های دﻳﮕﺮ ﻣﺎﻧﻨد ﻣﻌﻴﺎر بهینگی ﻛﻪ بهصورت ﻏﻴﺮﻣﺴﺘﻘﻴﻢ ﺑﻪ ﺣﻞ ﻳﻚ ﻣﺴﺌﻠﻪ بهینه¬سازی میپرداختند، توانایی ﺧﻮد را درزمینه¬ی ﺣﻞ ﻣﺴﺎﺋﻞ بهینهسازی توپوﻟﻮژي ﺑﺎ اﺑﻌﺎد واﻗﻌﻲ و ﻗﻴﻮد زﻳﺎد اﺛﺒﺎت ﻧﻤﻮدﻧﺪ. بهطورکلی روشهای بهینه¬سازی ﺗﻮﭘﻮﻟﻮژﻳﻜﻲ را می¬توان به دو ﮔﺮوه ﻋﻤﺪه ﺗﻘﺴﻴﻢ ﻧﻤﻮد.
ﮔﺮوه اول روشهای ﺑﺮ ﭘﺎﻳﻪ رﻳﺎﺿﻴﺎت ﺑﻮده و گروه دوم روشهای ﺗﻜﺎﻣﻠﻲ و ﺷﻬﻮدي است. از اﻧﻮاع روشهای ﻣﻄﺮح ﺑﺮ ﭘﺎﻳﻪ رﻳﺎﺿﻴﺎت میتوان ﺑﻪ روشهای همگنسازی و روش SIMP اﺷﺎره ﻧﻤﻮد. در روش همگنسازی، فضای ﻃﺮاحی به تعداد ﻣﻌﻴﻨﻲ ﺳﻠﻮل تقسیمشده ﻛﻪ ﻫﺮ ﻳﻚ از آنها بهعنوان یک رﻳﺰ ﺳﺎزه ﻣﺤﺴﻮب میشوند و میتوانند ﺧﺼﻮﺻﻴﺎت ﻣﺮﺑﻮط ﺑﻪ ﺧﻮد را داﺷﺘﻪ ﺑﺎﺷند. اﻳﻦ روش ضمن اینکه نتایج قابلتوجهی را ارائه مینماید اما دارای نقاط ضعفی از قبیل همگرا شدن به جوابهای بهینه محلی، روابط نسبتاً پیچیده ریاضی و پیدایش نواقصی از قبیل صفحه شطرنجی شدن و نواحی خاکستری در نتایج آن میباشد، هرچند که در سالهای بعد فیلترهای مختلف جهت حداقل کردن این مشکلات ارائه گردید. روشهای ریز سازههای ایزوتروپیک جامد با تابع جریمه که به روش SIMP مرسوم است به طور گستردهای در حل مسائل مختلف مورد استفاده قرار گرفت. یکی از مزیت¬های اﻳﻦ روش ﺣﺪاﻗﻞ ﺷﺪن ﭘﻮﺷﺶ ناقص ﻣﻮاد در رﻳﺰ سازهها و ﺣﺪاﻗﻞ ﺷﺪن ﭘﻴﺪاﻳﺶ ﻧﻮاﺣﻲ ﺧﺎﻛﺴﺘﺮي در ﻧﺘﺎﻳﺞ ﺑﻮد، هرچند ﻧﺘﺎﻳﺞ بهدستآمده از این روش ﻧﻴﺰ ﺗﺎ ﺣﺪودي ﺑﻪ ﻣﻘﺪار ﺗﻮان مورد استفاده در ﺗﺎﺑﻊ ﺟﺮیمه وابسته است. پیچیدگی رواﺑﻂ رﻳﺎﺿﻲ و ﺑﺮﺧﻲ دﻳﮕﺮ از ﻣﺸﻜﻼت ﻓﻮق ﻣﻨﺠﺮ ﺑﻪ اراﺋﻪ روشهای تکاملی ﮔﺮدﻳﺪ. روشهای ﺗﻜﺎﻣﻠﻲ ﺑﺎ ﺣﺬف ﺗﺪرﻳﺠﻲ ﻣﻮاد زاﺋﺪ از ﻓﻀﺎي ﻃﺮاﺣﻲ ﺑﻪ جواب موردنظر دﺳﺖ مییابند. ازجمله روشهای ﺗﻜﺎﻣﻠﻲ میتوان ﺑﻪ ﻣﻮاردي از ﻗﺒﻴﻞ ﺣﺪاﻛﺜﺮ ﺗﻨﺶ ﻃﺮاﺣﻲ ، ﻣﺮگ ﻧﺮم ، اﻓﺰاﻳﺶ ﻣﻌﻜﻮس و بهینه¬سازی ﺗﻜﺎﻣﻠﻲ سازه¬ها اﺷﺎره کرد. روش¬های تکاملی داراي مزایایی از قبیل سهولت نسبی در برنامه¬نویسی و درﮔﻴﺮ نشدن ﺑﺎ رواﺑﻂ ﭘﻴﭽﻴﺪه رﻳﺎﺿﻲ، ﻋﺪم پیدایش ﻧﻮاحی خاکستری و نزدیک بودن قابلتوجه نتایج بهدستآمده با نتایج تحلیلی می¬باشد.
در این فصل ایدههای اساسی و اصطلاحات فنی بهینهسازی سازهای معرفی میشود. نقش بهینهسازی ریاضی در فرایند طراحی محصول، فرمولبندیهای تودرتو و بهطور همزمان بهینهسازی سازهای، و سه طرح پایه پارامتر سازی هندسی اندازه، شکل و توپولوژی، مورد بحث قرار میگیرد. در این فصل و فصل بعد روشهای برنامهنویسی ریاضی برای حل مسائل با مقیاس بزرگ معرفی میشود. با مروری بر مبانی برنامهنویسی ریاضی تمرکز اصلی روی مسائل محدب است. باوجوداینکه در واقعیت اکثر مسائل بهینهسازی سازهای غیر محدب بوده، اما نمیتوان مسائل محدب را غیر مهم تلقی کرد. در فصل سوم مشخص میشود که تقریبهای کوژ نقش مهمی را در الگوریتم حل مسائل غیر محدب ایفا میکنند.

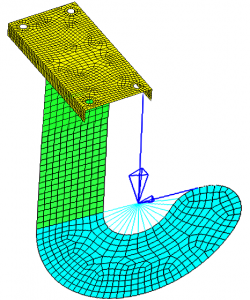
 توپولوژی تحلیل وضع و پیوند
توپولوژی تحلیل وضع و پیوند